
Concept explainers
(a)
To find: The value of
(a)
Answer to Problem 11E
The value of
Explanation of Solution
Given:
The company makes square wafers of silicon of area of the form
Calculation:
Differentiate the area of the square wafer respect to x.
Substitute 15 for
Therefore, the rate at which the area will increase with respect to change in its side length, if the side length is 15 mm will be
(b)
To Show: The rate of change of the area of a square with respect to the change in its side length is equal to half its perimeter.
(b)
Explanation of Solution
Draw the square with side length, x as shown in Figure (1).
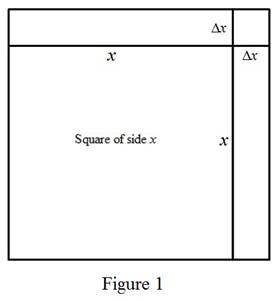
The perimeter of the square is
From the figure 1, the change in length
The first derivative of
Thus, the change in area of the square is approximately half of its perimeter which is half of the 4 sides times.
The expression for the shaded area (change in area) as below.
The change in length
The term
Thus the rate of change of the area of a square with respect to the change in its side length is equal to half its perimeter is
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





