
Concept explainers
(a)
(i)
The average rate of change of the area of a circle with respect to its radius
(a)
(i)
Answer to Problem 13E
The average rate of change of the area of a circle is
Explanation of Solution
Expression for the area of the circle is given as below.
Calculate the average rate of change of the area of a circle, when the radius changes from 2 to 3.
Therefore, the average rate of change of the area of a circle is
(ii)
The average rate of change of the area of a circle with respect to its radius
(ii)
Answer to Problem 13E
The average rate of change of the area of a circle is
Explanation of Solution
Calculate the average rate of change of the area of a circle, when the radius changes from 2 to 2.5.
Therefore, the average rate of change of the area of a circle is
(iii)
The average rate of change of the area of a circle with respect to its radius
(iii)
Answer to Problem 13E
The average rate of change of the area of a circle is
Explanation of Solution
Calculate the average rate of change of the area of a circle, when the radius changes from 2 to 2.1.
Therefore, the average rate of change of the area of a circle is
b)
The instantaneous rate of change when r = 2.
b)
Answer to Problem 13E
When r is 2 the instantaneous rate of change is
Explanation of Solution
Calculate the instantaneous rate of change when
Differentiate the above area equation,
Substitute the value
Therefore, when the value of
c)
To show: The rate of change of the area of a circle with respect to its radius is equal to the circumference of the circle and why it is geometrically true.
c)
Answer to Problem 13E
It is geometrically true. Hence, the resulting change in area
Explanation of Solution
Show that the rate of change of the area of a circle with respect to its radius is equal to the circumference of the circle.
Circumference of the circle is given as below.
First derivative of the area of the circle is given as below from the equation (1).
Compare both the equations (1) and (2).
Consider a circular ring of radius r and strip of thickness
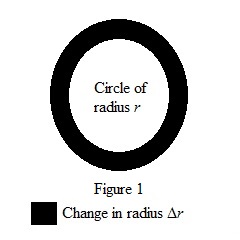
Show that if the value of
Explain why it is geometrically true.
Approximate the resulting change in area
Write the expression for
The value of
Hence, it is proved.
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





