
Concept explainers
(a)
To find: The sensitivity of the body.
(a)
Answer to Problem 32E
Sensitivity of the body is
The graph is plotted between x and y coordinates for both
Explanation of Solution
Given:
The experimental formula is shown below.
Calculation:
Calculate the sensitivity
Sensitivity is defined to be the rate of change of the reaction with respect to
Substitute
Apply the quotient rule below.
Substitute
Thus, the sensitivity of the body is
(b)
To illustrate: The part (a) by graphing both R and S as functions of x and comment on the values of
(b)
Explanation of Solution
Illustration:
Sketch the curve.
Calculate the value of
Substitute 0 for
Repeat the calculation of the value
Tabulate the value of
| 0.00 | 40.00 |
| 0.20 | 16.96 |
| 0.40 | 15.01 |
| 0.60 | 13.98 |
| 0.80 | 13.30 |
| 1.00 | 12.80 |
| 1.20 | 12.41 |
| 1.40 | 12.10 |
| 1.60 | 11.83 |
| 1.80 | 11.61 |
| 2.00 | 11.42 |
| 2.20 | 11.24 |
| 2.40 | 11.09 |
| 2.60 | 10.95 |
| 2.80 | 10.83 |
| 3.00 | 10.72 |
| 3.20 | 10.61 |
| 3.40 | 10.52 |
| 3.60 | 10.43 |
| 3.80 | 10.35 |
| 4.00 | 10.27 |
| 4.20 | 10.20 |
| 4.40 | 10.13 |
| 4.60 | 10.06 |
| 4.80 | 10.00 |
| 5.00 | 9.95 |
| 5.20 | 9.89 |
| 5.40 | 9.84 |
| 5.60 | 9.79 |
| 5.80 | 9.74 |
| 6.00 | 9.70 |
| 6.20 | 9.66 |
| 6.40 | 9.62 |
| 6.60 | 9.58 |
| 6.80 | 9.54 |
| 7.00 | 9.50 |
| 7.20 | 9.47 |
| 7.40 | 9.43 |
| 7.60 | 9.40 |
| 7.80 | 9.37 |
| 8.00 | 9.34 |
| 8.20 | 9.31 |
| 8.40 | 9.28 |
| 8.60 | 9.25 |
| 8.80 | 9.22 |
| 9.00 | 9.20 |
| 9.20 | 9.17 |
| 9.40 | 9.15 |
| 9.60 | 9.12 |
| 9.80 | 9.10 |
| 10.00 | 9.08 |
Calculate the value of
Substitute 0 for
Repeat the calculation of the value
Tabulate the value of
| 0.00 | 0 |
| 0.20 | -14.856 |
| 0.40 | -6.6235 |
| 0.60 | -4.0713 |
| 0.80 | -2.8659 |
| 1.00 | -2.176 |
| 1.20 | -1.7342 |
| 1.40 | -1.4297 |
| 1.60 | -1.2083 |
| 1.80 | -1.041 |
| 2.00 | -0.9106 |
| 2.20 | -0.8064 |
| 2.40 | -0.7215 |
| 2.60 | -0.6512 |
| 2.80 | -0.592 |
| 3.00 | -0.5417 |
| 3.20 | -0.4984 |
| 3.40 | -0.4609 |
| 3.60 | -0.428 |
| 3.80 | -0.399 |
| 4.00 | -0.3733 |
| 4.20 | -0.3503 |
| 4.40 | -0.3298 |
| 4.60 | -0.3112 |
| 4.80 | -0.2944 |
| 5.00 | -0.2791 |
| 5.20 | -0.2651 |
| 5.40 | -0.2524 |
| 5.60 | -0.2406 |
| 5.80 | -0.2298 |
| 6.00 | -0.2198 |
| 6.20 | -0.2105 |
| 6.40 | -0.2019 |
| 6.60 | -0.1939 |
| 6.80 | -0.1864 |
| 7.00 | -0.1795 |
| 7.20 | -0.1729 |
| 7.40 | -0.1668 |
| 7.60 | -0.161 |
| 7.80 | -0.1556 |
| 8.00 | -0.1505 |
| 8.20 | -0.1456 |
| 8.40 | -0.1411 |
| 8.60 | -0.1367 |
| 8.80 | -0.1326 |
| 9.00 | -0.1288 |
| 9.20 | -0.1251 |
| 9.40 | -0.1215 |
| 9.60 | -0.1182 |
| 9.80 | -0.115 |
| 10.00 | -0.112 |
Graph:
Sketch the curve using table (1) and table (2) as shown in figure (1).
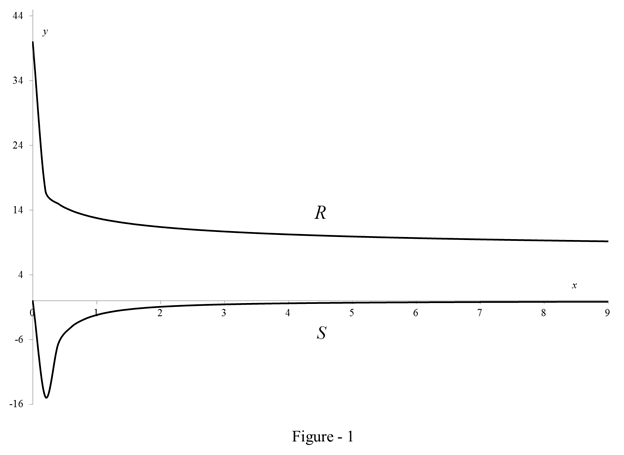
Refer the figure (1).
For all the small values of
Comments:
At low level of brightness, the eye is more sensitive to slight changes than it is at higher level of brightness.
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





