Science
ChemistryChemistry & Chemical ReactivityNicotinic acid, C 6 H 5 NO 2 , is found in minute amounts in all living cells, hut appreciable amounts occur in liver, yeast, milk, adrenal glands, white meat, and corn. Whole wheat (lour contains about 60. 0 μ g per gram of flour. One gram (1.00 g) of the acid dissolves in water to give 60. mL of solution having a pH of 2.70. What is the approximate value of K a for the acid? Nicotinic acid

Nicotinic acid, C 6 H 5 NO 2 , is found in minute amounts in all living cells, hut appreciable amounts occur in liver, yeast, milk, adrenal glands, white meat, and corn. Whole wheat (lour contains about 60. 0 μ g per gram of flour. One gram (1.00 g) of the acid dissolves in water to give 60. mL of solution having a pH of 2.70. What is the approximate value of K a for the acid? Nicotinic acid

BuyFind

Chemistry & Chemical Reactivity

10th Edition
John C. Kotz + 3 others
Publisher: Cengage Learning
ISBN: 9781337399074
BuyFind

Chemistry & Chemical Reactivity

10th Edition
John C. Kotz + 3 others
Publisher: Cengage Learning
ISBN: 9781337399074

Solutions

Chapter
Section
Problem 1PS
Problem 2PS
Problem 3PS
Problem 4PS
Problem 5PS
Problem 6PS
Problem 7PS
Problem 8PS
Problem 9PS
Problem 10PS
Problem 11PS
Problem 12PS
Problem 13PS
Problem 14PS
Problem 15PS
Problem 16PS
Problem 17PS
Problem 18PS
Problem 19PS
Problem 20PS
Problem 21PS
Problem 22PS
Problem 23PS
Problem 24PS
Problem 25PS
Problem 26PS
Problem 27PS
Problem 28PS
Problem 29PS
Problem 30PS
Problem 31PS
Problem 32PS
Problem 33PS
Problem 34PS
Problem 35PS
Problem 36PS
Problem 37PS
Problem 38PS
Problem 39PS
Problem 40PS
Problem 41PS
Problem 42PS
Problem 43PS
Problem 44PS
Problem 45PS
Problem 46PS
Problem 47PS
Problem 48PS
Problem 49PS
Problem 50PS
Problem 51PS
Problem 52PS
Problem 53PS
Problem 54PS
Problem 55PS
Problem 56PS
Problem 57PS
Problem 58PS
Problem 59PS
Problem 60PS
Problem 61PS
Problem 62PS
Problem 63PS
Problem 64PS
Problem 65PS
Problem 66PS
Problem 67PS
Problem 68PS
Problem 69PS
Problem 70PS
Problem 71PS
Problem 72PS
Problem 73PS
Problem 74PS
Problem 75PS
Problem 76PS
Problem 77PS
Problem 78PS
Problem 79PS
Problem 80PS
Problem 81PS
Problem 82PS
Problem 83PS
Problem 84PS
Problem 85GQ
Problem 86GQ
Problem 87GQ
Problem 88GQ
Problem 89GQ
Problem 90GQ
Problem 91GQ
Problem 92GQ
Problem 93GQ
Problem 94GQ
Problem 95GQ
Problem 96GQ
Problem 97GQ
Problem 98GQ
Problem 99GQ
Problem 100GQ
Problem 101GQ
Problem 102GQ
Problem 103GQ
Problem 104GQ
Problem 105GQ
Problem 106GQ
Problem 107GQ
Problem 108GQ
Problem 109GQ
Problem 110GQ
Problem 111IL
Problem 112IL
Problem 113IL
Problem 114IL
Problem 115IL
Problem 116IL
Problem 117IL
Problem 118IL
Problem 119SCQ
Problem 120SCQ
Problem 121SCQ
Problem 122SCQ
Problem 123SCQ
Problem 124SCQ
Problem 125SCQ
Problem 126SCQ
Problem 127SCQ
Problem 128SCQ
Problem 129SCQ
Chapter 16, Problem 115IL
Textbook Problem

Nicotinic acid, C6H5NO2, is found in minute amounts in all living cells, hut appreciable amounts occur in liver, yeast, milk, adrenal glands, white meat, and corn. Whole wheat (lour contains about 60. 0μg per gram of flour. One gram (1.00 g) of the acid dissolves in water to give 60. mL of solution having a pH of 2.70. What is the approximate value of Ka for the acid?

Chapter 16, Problem 115IL, Nicotinic acid, C6H5NO2, is found in minute amounts in all living cells, hut appreciable amounts

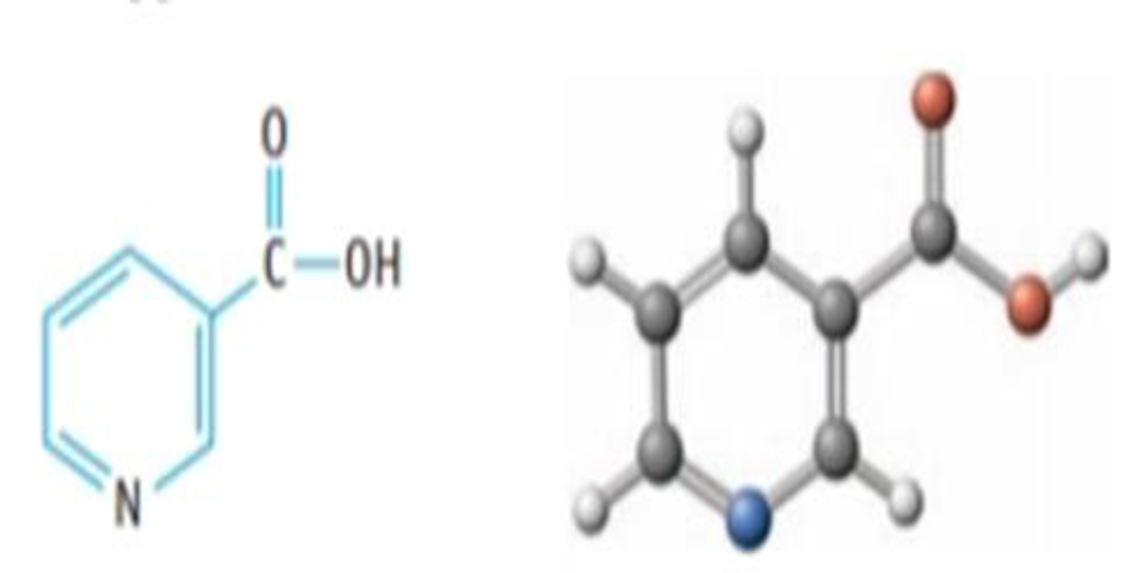
Nicotinic acid

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.
Chapter 16,
Problem 114IL
Chapter 16,
Problem 116IL

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 16 Solutions

Chemistry & Chemical Reactivity
Ch. 16.2 - What are the hydronium ion and hydroxide ion...Ch. 16.4 - For each of the following salts in water, predict...Ch. 16.5 - (a) Which is the stronger Bronsted acid, HCO3 or...Ch. 16.7 - A solution prepared from 0.055 mol of butanoic...Ch. 16.7 - What are the equilibrium concentrations of acetic...Ch. 16.7 - What are the equilibrium concentrations of HF, F...Ch. 16.7 - The weak base, CIO (hypochlorite ion), is used in...Ch. 16.7 - Calculate the pH after mixing 15 mL of 0.12 M...Ch. 16.8 - What is the pH of a 0.10 M solution of oxalic...Ch. 16.10 - If a fatal does of atropine is 100. mg. what...Ch. 16.10 - When atropine is added to sulfuric acid, a proton...Ch. 16.10 - The pKa, of the conjugate acid of atropine is...Ch. 16.10 - Convert the pK values to K values for the...Ch. 16.10 - Other solvents also undergo autoionization. (a)...Ch. 16.10 - Write an equation for the reaction of the amide...Ch. 16.10 - Will a solution of HClO4 in glacial acetic acid be...Ch. 16.10 - To measure the relative strengths of bases...Ch. 16 - Write the formula and the give the name of the...Ch. 16 - Write the formula and give the name of the...Ch. 16 - What are the products of each of the following...Ch. 16 - What are the products of each of the following...Ch. 16 - Write balanced equations showing how the hydrogen...Ch. 16 - Write a balanced equation showing how the HPO42...Ch. 16 - In each of the following acid-base reactions,...Ch. 16 - In each of the following acid-base reactions,...Ch. 16 - An aqueous solution has a pH of 3.75. What is the...Ch. 16 - A saturated solution of milk of magnesia. Mg(OH)2,...Ch. 16 - What is the pH of a 0.0075 M solution of HCl? What...Ch. 16 - What is the pH of a 1.2 104 M solution of KOH?...Ch. 16 - What is the pH of a 0.0015 M solution of Ba(OH)2?Ch. 16 - The pH of a solution of Ba(OH)2 is 10.66 at 25 ....Ch. 16 - Write an equilibrium constant expression for the...Ch. 16 - Write an equilibrium constant expression for the...Ch. 16 - Several acids are listed here with their...Ch. 16 - Several acids are listed here with their...Ch. 16 - Which of the following ions or compounds has the...Ch. 16 - Which of the following compounds or ions has the...Ch. 16 - Which of the following compounds or ions has the...Ch. 16 - Which of the following compounds or ion has the...Ch. 16 - Dissolving K2CO3 in water gives a basic solution....Ch. 16 - Dissolving ammonium bromide in water gives an...Ch. 16 - If each of the salts listed here were dissolved in...Ch. 16 - Which of the following common food additives gives...Ch. 16 - A weak acid has a Ka of 6.5 105 What is the value...Ch. 16 - If Ka for weak acid is 2.4 1011, what is the...Ch. 16 - Epinephrine hydrochloride has pKa value of 9.53....Ch. 16 - An organic acid has pKa = 8.95. What is its Ka...Ch. 16 - Which is the stronger of the following two acids?...Ch. 16 - Which is the stronger of the following two acids?...Ch. 16 - Chloroacetic acid (ClCH2CO2H) has Ka = 1.41 103....Ch. 16 - A weak base has Kb = 1.5 109. What is the value...Ch. 16 - The trimethylammonium ion, (CH3)3NH+, is the...Ch. 16 - The chromium(III) ion in water, [Cr(H2O)6]3+. Is a...Ch. 16 - Acetic acid and sodium hydrogen carbonate, NaHCO3,...Ch. 16 - Ammonium chloride and sodium dihydrogen phosphate,...Ch. 16 - For each of the following reactions, predict...Ch. 16 - For each of the following reactions, predict...Ch. 16 - Equal molar quantities of sodium hydroxide and...Ch. 16 - Equal molar quantities of hydrochloric acid and...Ch. 16 - Equal molar quantities of acetic acid and sodium...Ch. 16 - Equal molar quantities of ammonia and sodium...Ch. 16 - A 0.015 M solution of hydrogen cyanate, HOCN, has...Ch. 16 - A 0.10 M solution of chloroacetic acid, CICH2CO2H,...Ch. 16 - A 0.025 M solution of hydroxyl amine has a pH of...Ch. 16 - Methylamine, CH3NH2, is a weak base. CH3NH2(aq) +...Ch. 16 - A 2.5 103 M solution of an unknown acid has a pH...Ch. 16 - A 0.015M solution of a base has a pH of 10.09 a)...Ch. 16 - What are the equilibrium concentrations of...Ch. 16 - The ionizations constant of a very weak acid, HA...Ch. 16 - What are the equilibrium concentration of H3O+, CN...Ch. 16 - Phenol (C6H5OH) commonly called carbolic acid is a...Ch. 16 - What are the equilibrium concentrations of...Ch. 16 - A hypothetical weak base has Kb=5.0104.Calculate...Ch. 16 - The weak base methylamine, CH3NH2, has Kb=4.2104....Ch. 16 - Calculate the pH of a 0.12 M aqueous solution of...Ch. 16 - Calculate the pH of a 0.0010 M aqueous solution of...Ch. 16 - A solution of hydrofluoric acid, HF, has a pH of...Ch. 16 - Calculate the hydronium ion concentration and pH...Ch. 16 - Calculate the hydronium ion concentration and pH...Ch. 16 - Sodium cyanide is the salt of the weak acid HCN....Ch. 16 - The sodium salt of propionic acid, NaCH3CH2CO2 is...Ch. 16 - Calculate the hydronium ion concentration and pH...Ch. 16 - Calculate the hydronium ion concentration and the...Ch. 16 - For each of the following cases, decide whether...Ch. 16 - For each of the following cases, decide whether...Ch. 16 - Oxalic acid, H2C2O4, is a diprotic acid. Write a...Ch. 16 - Sodium carbonate is a diprotic base. Write a...Ch. 16 - Prove that Ka1 Kb2 = Kw for oxalic acid H2C2O4,...Ch. 16 - Prove that Ka3 Kb1 = Kw for phosphoric acid,...Ch. 16 - Sulphurous acid, H2SO3, is a weak acid capable of...Ch. 16 - Ascorbic acid (vitamin C, C6H8O6) is a diprotic...Ch. 16 - Hydrazine, N2H4, can interact with water in two...Ch. 16 - Ethylene diamine, H2NCH2CH2NH2, can interact with...Ch. 16 - Which should be stronger acid, HOCN or HCN?...Ch. 16 - Which should be the stronger Brnsted acid,...Ch. 16 - Explain why benzene sulfonic acid is a Brnsted...Ch. 16 - The structure of ethylene diamine is illustrated...Ch. 16 - Decide whether each of the following substances...Ch. 16 - Decide whether each of the following substances...Ch. 16 - Carbon monoxide forms complexes with low-valent...Ch. 16 - Trimethylamine, (CH3)3N, is a common reagent. It...Ch. 16 - About this time, you may be wishing you had an...Ch. 16 - Consider the following ions: NH4+, CO32, Br, S2,...Ch. 16 - A 2.50 g sample of a solid that could be Ba(OH)2...Ch. 16 - In a particular solution, acetic acid is 11%...Ch. 16 - Hydrogen, H2S, and sodium acetate, NaCH3CO2 are...Ch. 16 - For each of the following reactions predict...Ch. 16 - A monoprotic acid HX has Ka = 1.3 103. Calculate...Ch. 16 - Arrange the following 0.10M solutions in order of...Ch. 16 - m-Nitrophenol, a weak acid, can be used as a pH...Ch. 16 - The butylammonium ion, C4H9NH3+, has a Ka of 2.3 ...Ch. 16 - The local anaesthetic novocaine is the hydrogen...Ch. 16 - Pyridine is weak organic base and readily forms a...Ch. 16 - The base ethylamine (CH3CH2NH2) has a Kb of. A...Ch. 16 - Chloroacetic acid, ClCH2CO2H, is a moderately weak...Ch. 16 - Saccharin (HC7H4NO3S) is a weak acid with pKa =...Ch. 16 - Given the following solutions: (a) 0.1 M NH3 (b)...Ch. 16 - For each of the following salts, predict whether a...Ch. 16 - Nicotine, C10H14N2, has two basic nitrogen atoms...Ch. 16 - Oxalic acid is a relatively weak diprotic acid....Ch. 16 - The equilibrium constant for the reaction of...Ch. 16 - The equilibrium constant for the reaction of...Ch. 16 - Calculate the pH of the solution that results from...Ch. 16 - To what volume should 1.00 102 mL of any weak...Ch. 16 - The hydrogen phthalate ion, C8HsO4, is a weak acid...Ch. 16 - You prepare a 0.10 M solution of oxalic acid,...Ch. 16 - You mix 30 0 mL of 0.15 M NaOH with 30.0 mL of...Ch. 16 - Describe an experiment that will allow you to...Ch. 16 - The data below compare the strength of acetic acid...Ch. 16 - You have three solutions labeled A, B, and C. You...Ch. 16 - A hydrogen atom in the organic base pyridine,...Ch. 16 - Nicotinic acid, C6H5NO2, is found in minute...Ch. 16 - Equilibrium constants can be measured for the...Ch. 16 - Sulfanilic acid, which is used in making dyes, is...Ch. 16 - Amino acids are an important group of compounds....Ch. 16 - How can water be both a Brnsied base and a Lewis...Ch. 16 - The nickel(II) ion exists as [Ni(H2O)4]2+ in...Ch. 16 - The halogens form three stable, weak acids, HOX....Ch. 16 - The acidity of the oxoacids was described in...Ch. 16 - Perchloric acid behaves as an acid, even when it...Ch. 16 - You purchase a bottle of water. On checking its...Ch. 16 - Iodine, I2, is much more soluble in an aqueous...Ch. 16 - Uracil is a base found in RNA Indicate sites in...Ch. 16 - Chemists often refer to the decree of ionization...Ch. 16 - Exploring the degree of ionization equation in...Ch. 16 - Consider a salt of a weak base and a weak acid...

Additional Science Textbook Solutions

Find more solutions based on key concepts
Naturally occurring nitrogen is a mixture of 14N and 15N. Give the number of protons, neutrons, and electrons i...

General Chemistry - Standalone book (MindTap Course List)

Explain what the “duet" and “octet” rules are and how they are used to describe the arrangement of electrons in...

Introductory Chemistry: A Foundation

Commercial cold packs and hot packs are available for treating athletic injuries. Both types contain a pouch of...

Chemistry

Complete the following table. Atmos Number of Protons Number of Neutrons H24e N1020e T2248i O76190s C27...

Chemistry: An Atoms First Approach

Can a monohybrid cross be used to illustrate Mendels principle of independent assortment?

Biology (MindTap Course List)

Calculate which food provides more riboflavin per 1-ounce servinga pork chop (3 oz, 291 kcal, 0.25 mg riboflavi...

Understanding Nutrition (MindTap Course List)

Consider the 12.0 kg motorcycle wheel shown in Figure 10.38. Assume it to be approximately an annular ring with...

College Physics

Dietary Fat Overload Reprograms Mitochondria The bodies of humans and other mammals store triglycerides in two ...

Biology: The Unity and Diversity of Life (MindTap Course List)

List three reasons why someone might take a multivitamin supplement that does not exceed 100 percent of the RDA...

Nutrition: Concepts and Controversies - Standalone book (MindTap Course List)

FIGURE 10.8 Recently erupted basaltic lava on the island of Hawaii. Molten basalt typically erupts at very high...

Fundamentals of Physical Geography

One mile is equal to 1,609 m. Express this distance in kilometers and in centimeters.

Inquiry into Physics

A ladder 9.00 m long leans against the side of a building. If the ladder is inclined at an angle of 75.0 to the...

College Physics

To plan a healthy diet that correctly assigns the needed amounts of food from each food group, the diet planner...

Nutrition

9. Explain the importance of each of the following locations with respect to the Manhattan Project: a. Los Alam...

Chemistry In Focus

If the DNA strand in a molecule could be stretched out, it would have a length on the order of 2.0 m. What woul...

An Introduction to Physical Science

Estimate the temperature range over which each of the following reactions is spontaneous. (a) 2Al(s)+3Cl2(g)2Al...

Chemistry for Engineering Students

Indicate whether each of the following statements is true or false. If the statement is false, restate it to ma...

Chemistry: Principles and Reactions

Match each item with its description. ____ tendon a. stores and releases calcium ____ Z line b. all in the hand...

BIOLOGY:CONCEPTS+APPL.(LOOSELEAF)

24-37 What is the direct target of the second messenger produced when glucagon binds to its receptor?

Introduction to General, Organic and Biochemistry

7. Which of the following has the greatest combined cross-sectional area? A. Terminal bronchioles B. Labar ...

Cardiopulmonary Anatomy & Physiology

Name two strategies for decreasing a school-age childs sedentary behaviors.

Nutrition Through The Life Cycle

What is physically exchanged during crossing over?

Human Heredity: Principles and Issues (MindTap Course List)

Answers to all problems are at the end of this book. Detailed solutions are available in the Student Solutions ...

Biochemistry

You are packing for a vacation on a planet orbiting another star that is much like the Sun. Why might you want ...

Horizons: Exploring the Universe (MindTap Course List)

REFLECT AND APPLY Comment on the dual role of the monomeric reactants in replication.

Biochemistry

Given what you now know about how foreign invaders trigger immune responses, explain why mutated forms of virus...

Human Biology (MindTap Course List)

What is a life cycle?

Biology: The Dynamic Science (MindTap Course List)

A steel tank with a volume of 6.25L is full of gas at a pressure of 3.25atm. What volume in liters would the ga...

Chemistry for Today: General, Organic, and Biochemistry

Use the following data (in kJ/mol) to estimate E for the reaction S(g)+e S2(g). Include an estimate of uncerta...

Chemistry

21. List the four major components of smog and the effects of each.

Chemistry In Focus

Consider an aqueous solution of a polymer that has an average molecular weight of 185,000amu. Calculate the mol...

Physical Chemistry

Use rise web to look up the percentage of dopant for a commercially available p-type semiconductor. Imagine tha...

Chemistry for Engineering Students

Newtons law of universal gravitation is represented by F=GMmr2 where F is the gravitational force, M and m are ...

College Physics

Explain why you agree or disagree with each of the following statements: (a) humans are superior to other forms...

Environmental Science (MindTap Course List)

Rank the following compounds in order of their expected reactivity toward SN2 reaction: CH3Br, CH3OTos, (CH3)3C...

Organic Chemistry

Famine during pregnancy is associated with pSGA at birth and increased risk of heart disease, stroke, and type ...

Nutrition Through the Life Cycle (MindTap Course List)

Determine the following, using the periodic table given in Problem 3-63. a. Is the element highlighted in yello...

General, Organic, and Biological Chemistry

Two gliders are set in motion on a horizontal air track. A light spring of force constant k is attached to the ...

Physics for Scientists and Engineers

Consider the accompanying graph, which compares the losses of calcium from the experimental and control sites i...

Environmental Science (MindTap Course List)

Indicate whether each of the following pairings of concepts related to regulation of enzyme activity is a corre...

Organic And Biological Chemistry

Following is a retrosynthetic scheme for the synthesis of cis-3-penten-2-ol. Write a synthesis for this compoun...

Organic Chemistry

Consider the following half reactions: Cd2+(aq)+2eCd(s); Pb2+(aq)+2ePb(s); Cl2(g)+2e2Cl(aq). Identify the stron...

Introductory Chemistry: An Active Learning Approach

Through _______, a body part of an ancestor is modified differently in different lines of descent. a. homologou...

Biology: The Unity and Diversity of Life (MindTap Course List)

Figure P12.13 shows a claw hammer being used to pull a nail out of a horizontal board. The mass of the hammer i...

Physics for Scientists and Engineers with Modern Physics

What is environmental resistance? What sort of a growth curve would you expect from an organism placed in a hab...

Oceanography: An Invitation To Marine Science, Loose-leaf Versin

Two transverse sinusoidal waves combining in a medium are described by the wave functions y1 = 3.00 sin (x + 0....

Physics for Scientists and Engineers, Technology Update (No access codes included)

When Tycho observed the new star of 1572, he could detect no parallax. Why did that undermine belief in the Pto...

Foundations of Astronomy (MindTap Course List)

Police measure the speed of moving vehicles with radar guns. A radar gun sends out radio waves with a typical f...

Physics for Scientists and Engineers: Foundations and Connections

A scientist compares the plasma membrane composition of an animal from the Mediterranean coast with one from th...

Biology 2e

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.