
Concept explainers
Area of a Box An open box with a square base is to have a volume of 12 ft3.
- (a) Find a function that models the surface area of the box.
- (b) Find the box dimensions that minimize the amount of material used.
(a)
To find: The function that models the surface area of a open box with square base whose volume is
Answer to Problem 27P
The function that models the surface area of given box is
Explanation of Solution
Let the dimension of square base be x and height h
Surface area
Volume of the box is,
Substitute 12 for
Divide both sides of above equation by
Summarize all the information as shown in the table below.
| In Words | In Algebra |
| Surface Area |
|
| Length of side of square base. |
|
| Height of the box |
|
Use the information in the table and model the function.
Thus, the function that models the surface area of given box is
(b)
To find: The dimensions of the box which minimize the material used to make the box.
Answer to Problem 27P
The length of square base of box is approximately
Explanation of Solution
The function as calculated in part (a) is,
Sketch the graph of above function as shown below.
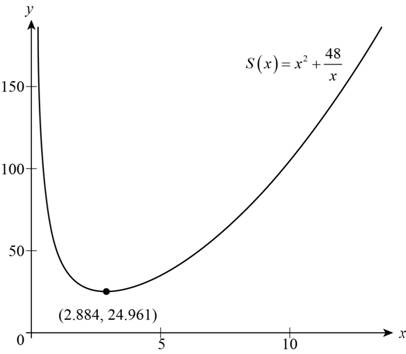
Figure (1)
Observe from the graph shown in Figure (1) that it attains minimum value at
Length of square base is
Height of box as calculated in terms of length of base in part (a) is,
Substitute
Thus, the length of square base of box is approximately
Chapter 2 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





