Precalculus: Mathematics for Calculus - 6th Edition
Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Question
Book Icon
Chapter 2.3, Problem 31E

a.

To determine

To find all the local maximum and minimum value of the function and the value of x at which each occur using the graph of the function given.

a.

Expert Solution
Check Mark

Answer to Problem 31E

The local maximum and minimum value of the function are 2 and −1,0 respectively and the value of x at which each occur are 0 and −2,2 respectively.

Explanation of Solution

Given information :

The graph of the function is given.

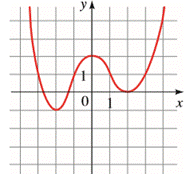
  Precalculus: Mathematics for Calculus - 6th Edition, Chapter 2.3, Problem 31E , additional homework tip 1

Draw a viewing rectangle on each of the extremum of the graph of the function which is provided in the question.

The graph is shown below:

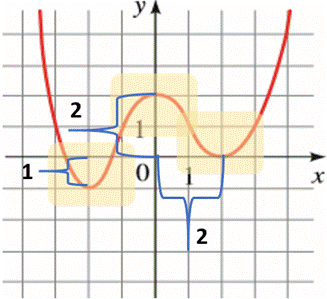
  Precalculus: Mathematics for Calculus - 6th Edition, Chapter 2.3, Problem 31E , additional homework tip 2

From the above graph, it can be observed that the point (0,f(0)) is the highest point on the graph of f within the viewing rectangle, so the number f(0)=2 is a local maximum value of the function.

Similarly, it can be observed that the point (−2,f(−2)) and (2,f(2)) are the lowest points on the graph of f within the viewing rectangle, so the numbers f(−2)=−1 and f(2)=0 are the local minimum value of the function.

Hence,

The local maximum and minimum value of the function are 2 and −1,0 respectively and the value of x at which each occur are 0 and −2,2 respectively.

b.

To determine

To find the interval on which the function is increasing and on which the function is decreasing.

b.

Expert Solution
Check Mark

Answer to Problem 31E

The function f is decreasing on (−∞,−2] and [0,2] and increasing on [−2,0] and [2,∞) .

Explanation of Solution

Given information :

The graph of the function is given.

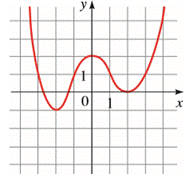
  Precalculus: Mathematics for Calculus - 6th Edition, Chapter 2.3, Problem 31E , additional homework tip 3

Concept used:

The function is increasing on an interval I if f(x1)<f(x2) whenever x1<x2 in I .

The function is decreasing on an interval I if f(x1)>f(x2) whenever x1<x2 in I .

The graph of the function is shown below:

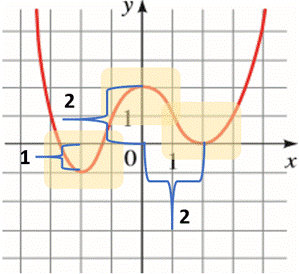
  Precalculus: Mathematics for Calculus - 6th Edition, Chapter 2.3, Problem 31E , additional homework tip 4

Use definition of increasing and decreasing function.

From the above graph, it can be observed that the function f is decreasing on (−∞,−2] and [0,2] as f(−∞)=∞>f(−2)=−1 for −∞<−2 and f(0)=2>f(2)=0 for 0<2 respectively. and increasing on [−2,0] and [2,∞) as f(−2)=−1<f(0)=2 for −2<0 and f(2)=0<f(∞)=∞ for 2<∞ respectively.

Previous
Chapter 2.3, Problem 30E
Next
Chapter 2.3, Problem 32E

Chapter 2 Solutions

Precalculus: Mathematics for Calculus - 6th Edition

Ch. 2.1 - Prob. 1ECh. 2.1 - For a function f, the set of all possible inputs...Ch. 2.1 - (a) Which of the following functions have 5 in...Ch. 2.1 - A function is given algebraically by the formula...Ch. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - Prob. 63ECh. 2.1 - Prob. 64ECh. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Prob. 69ECh. 2.1 - Prob. 70ECh. 2.1 - Prob. 71ECh. 2.1 - Prob. 72ECh. 2.1 - Prob. 73ECh. 2.1 - Prob. 74ECh. 2.1 - Relativity According to the Theory of Relativity,...Ch. 2.1 - Income Tax In a certain country, income tax T is...Ch. 2.1 - Internet Purchases An Internet bookstore charges...Ch. 2.1 - Cost of a Hotel Stay A hotel chain charges 75 each...Ch. 2.1 - Speeding Tickets In a certain state the maximum...Ch. 2.1 - Height of Grass A home owner mows the lawn every...Ch. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.1 - Prob. 85ECh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Match the function with its graph. (a) f(x) = x2...Ch. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Weather Balloon As a weather balloon is inflated,...Ch. 2.2 - Power from a Wind Turbine The power produced by a...Ch. 2.2 - Utility Rates Westside Energy charges its electric...Ch. 2.2 - Taxicab Function A taxi company charges 2.00 for...Ch. 2.2 - Prob. 83ECh. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Earthquake The graph shows the vertical...Ch. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Hurdle Race Three runners compete in a 100-meter...Ch. 2.3 - Gravity Near the Moon We can use Newtons Law of...Ch. 2.3 - Prob. 51ECh. 2.3 - Migrating Fish A fish swims at a speed v relative...Ch. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Coughing When a foreign object that is lodged in...Ch. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.4 - If you travel 100 miles in two hours, then your...Ch. 2.4 - The average rate of change of a function f between...Ch. 2.4 - The average rate of change of the function f(x) =...Ch. 2.4 - (a) The average rate of change of a function f...Ch. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Changing Water Levels The graph shows the depth of...Ch. 2.4 - Population Growth and Decline The graph shows the...Ch. 2.4 - Population Growth and Decline The table gives the...Ch. 2.4 - Running Speed A man is running around a circular...Ch. 2.4 - Prob. 27ECh. 2.4 - Book Collection Between 1980 and 2000 a rare book...Ch. 2.4 - Cooling Soup When a bowl of hot soup is left in a...Ch. 2.4 - Farms in the United States The graph gives the...Ch. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.5 - Fill in the blank with the appropriate direction...Ch. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Prob. 66ECh. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - Prob. 78ECh. 2.5 - Prob. 79ECh. 2.5 - Prob. 80ECh. 2.5 - Prob. 81ECh. 2.5 - Prob. 82ECh. 2.5 - Prob. 83ECh. 2.5 - Prob. 84ECh. 2.5 - Prob. 85ECh. 2.5 - Prob. 86ECh. 2.5 - Prob. 87ECh. 2.5 - Prob. 88ECh. 2.5 - Prob. 89ECh. 2.5 - Prob. 90ECh. 2.5 - Prob. 91ECh. 2.5 - Prob. 92ECh. 2.5 - Prob. 93ECh. 2.6 - From the graphs of f and g in the figure, we find...Ch. 2.6 - By definition, (f g)(x) = _____. So if g(2) = 5...Ch. 2.6 - If the rule of the function f is add one and the...Ch. 2.6 - We can express the functions in Exercise 3...Ch. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.6 - Prob. 51ECh. 2.6 - Prob. 52ECh. 2.6 - Prob. 53ECh. 2.6 - Prob. 54ECh. 2.6 - Prob. 55ECh. 2.6 - Prob. 56ECh. 2.6 - Prob. 57ECh. 2.6 - Prob. 58ECh. 2.6 - Prob. 59ECh. 2.6 - Revenue, Cost, and Profit A print shop makes...Ch. 2.6 - Area of a Ripple A stone is dropped in a lake,...Ch. 2.6 - Inflating a Balloon A spherical balloon is being...Ch. 2.6 - Area of a Balloon A spherical weather balloon is...Ch. 2.6 - Multiple Discounts You have a 50 coupon from the...Ch. 2.6 - Multiple Discounts An appliance dealer advertises...Ch. 2.6 - Airplane Trajectory An airplane is flying at a...Ch. 2.6 - Prob. 67ECh. 2.6 - Prob. 68ECh. 2.6 - Prob. 69ECh. 2.6 - Prob. 70ECh. 2.7 - A function f is one-to-one if different inputs...Ch. 2.7 - (a) For a function to have an inverse, it must be...Ch. 2.7 - A function f has the following verbal description:...Ch. 2.7 - True or false? (a) If f has an inverse, then f1(x)...Ch. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - Prob. 51ECh. 2.7 - Prob. 52ECh. 2.7 - Prob. 53ECh. 2.7 - Prob. 54ECh. 2.7 - Prob. 55ECh. 2.7 - Prob. 56ECh. 2.7 - Prob. 57ECh. 2.7 - Prob. 58ECh. 2.7 - Prob. 59ECh. 2.7 - Prob. 60ECh. 2.7 - Prob. 61ECh. 2.7 - Prob. 62ECh. 2.7 - Prob. 63ECh. 2.7 - Prob. 64ECh. 2.7 - Prob. 65ECh. 2.7 - Prob. 66ECh. 2.7 - Prob. 67ECh. 2.7 - Prob. 68ECh. 2.7 - Prob. 69ECh. 2.7 - Prob. 70ECh. 2.7 - Prob. 71ECh. 2.7 - Prob. 72ECh. 2.7 - Prob. 73ECh. 2.7 - Prob. 74ECh. 2.7 - Prob. 75ECh. 2.7 - Prob. 76ECh. 2.7 - Prob. 77ECh. 2.7 - Prob. 78ECh. 2.7 - Prob. 79ECh. 2.7 - Prob. 80ECh. 2.7 - Fee for Service For his services, a private...Ch. 2.7 - Prob. 82ECh. 2.7 - Prob. 83ECh. 2.7 - Prob. 84ECh. 2.7 - Prob. 85ECh. 2.7 - Prob. 86ECh. 2.7 - Income Tax In a certain country the tax on incomes...Ch. 2.7 - Prob. 88ECh. 2.7 - Prob. 89ECh. 2.7 - Prob. 90ECh. 2.7 - Prob. 91ECh. 2.7 - Prob. 92ECh. 2.7 - Prob. 93ECh. 2 - Prob. 1RCCCh. 2 - Prob. 2RCCCh. 2 - Prob. 3RCCCh. 2 - Prob. 4RCCCh. 2 - Prob. 5RCCCh. 2 - Prob. 6RCCCh. 2 - Prob. 7RCCCh. 2 - Prob. 8RCCCh. 2 - Prob. 9RCCCh. 2 - Prob. 10RCCCh. 2 - Prob. 11RCCCh. 2 - Prob. 12RCCCh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Prob. 79RECh. 2 - Prob. 80RECh. 2 - Prob. 81RECh. 2 - Prob. 82RECh. 2 - Prob. 83RECh. 2 - Prob. 84RECh. 2 - Prob. 85RECh. 2 - Prob. 86RECh. 2 - Prob. 87RECh. 2 - Prob. 88RECh. 2 - Prob. 89RECh. 2 - Prob. 90RECh. 2 - Prob. 91RECh. 2 - Prob. 92RECh. 2 - Prob. 1TCh. 2 - Prob. 2TCh. 2 - A function f has the following verbal description:...Ch. 2 - A school fund-raising group sells chocolate bars...Ch. 2 - Prob. 5TCh. 2 - Prob. 6TCh. 2 - Prob. 7TCh. 2 - Prob. 8TCh. 2 - Prob. 9TCh. 2 - Prob. 10TCh. 2 - Prob. 11TCh. 2 - Prob. 12TCh. 2 - Prob. 1PCh. 2 - Prob. 2PCh. 2 - Prob. 3PCh. 2 - Prob. 4PCh. 2 - Prob. 5PCh. 2 - Prob. 6PCh. 2 - Prob. 7PCh. 2 - Prob. 8PCh. 2 - Prob. 9PCh. 2 - Prob. 10PCh. 2 - Prob. 11PCh. 2 - Length A woman 5 ft tall is standing near a street...Ch. 2 - Distance Two ships leave port at the same time....Ch. 2 - Prob. 14PCh. 2 - Area An isosceles triangle has a perimeter of 8...Ch. 2 - Prob. 16PCh. 2 - Area A rectangle is inscribed in a semicircle of...Ch. 2 - Height The volume of a cone is 100 in3. Find a...Ch. 2 - Prob. 19PCh. 2 - Minimizing a Sum Find two positive numbers whose...Ch. 2 - Prob. 21PCh. 2 - Dividing a Pen A rancher with 750 ft of fencing...Ch. 2 - Fencing a Garden Plot A property owner wants to...Ch. 2 - Maximizing Area A wire 10 cm long is cut into two...Ch. 2 - Light from a Window A Norman window has the shape...Ch. 2 - Volume of a Box A box with an open top is to be...Ch. 2 - Area of a Box An open box with a square base is to...Ch. 2 - Inscribed Rectangle Find the dimensions that give...Ch. 2 - Minimizing Costs A rancher wants to build a...Ch. 2 - Minimizing Time A man stands at a point A on the...Ch. 2 - Bird Flight A bird is released from point A on an...Ch. 2 - Area of a Kite A kite frame is to be made from six...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY