
a.
To explain why the
a.
Answer to Problem 58E
The local
Explanation of Solution
Given information:
the function is
The local maxima of
Similarly,
The local minima of
Hence,
The local maxima and minima of
b.
To express
b.
Answer to Problem 58E
Explanation of Solution
Given information:
Formula used:
Distance between two point
Calculation:
Therefore,
Use distance formula,
Hence,
c.
To find the minimum value of the function
c.
Answer to Problem 58E
The minimum value of the function
Explanation of Solution
Given information:
Calculation:
The function is
Use the principle describe in part (a) that the local maxima and minima of
Compare
The graph of
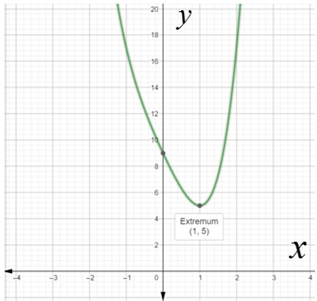
There appears to be one local minimum at
Hence,
Using maximum command, the local minimum value of
Since, the local maxima and minima of
Hence, localminima of
So, the minimum value of
Hence,
The minimum value of the function
Chapter 2 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





