
(a)
To find: The slope of the tangent line to the curve
(a)
Answer to Problem 4E
The slope of the tangent line to the curve
(i) Using Definition 1 is
(ii) Using Equation 2 is
Explanation of Solution
Given:
The equation of the curve
The slope of the tangent line to the curve at the point
Formula used:
Definition 1: The slope of the tangent curve
Equation 2: The slope of the tangent line in definition 1 becomes,
Difference of square formula:
Calculation:
Section (i)
Obtain the slope of the tangent line to the curve at the point (1, 0) using Definition 1.
Substitute
Apply the difference of squares formula,
Since the limit x approaches 1 but not equal to 1, cancel the common term
Thus, the slope of the tangent line to the parabola at the point (1, 0) by using Definition 1 is
Section (ii)
Obtain the slope of the tangent line to the parabola at the point (1, 0) by using Equation 2.
Substitute
Simplify the terms by expanding
Since the limit h approaches 0 but not equal to 0, cancel the common term
Thus, the slope of the tangent line to the parabola at the point (1, 0) by using Equation 2 is
(b)
To find: The equation of the tangent line in part (a).
(b)
Answer to Problem 4E
The equation of the tangent line in part (a) is
Explanation of Solution
Formula used:
The equation of the tangent line to the curve
Calculation:
Obtain the equation of the tangent line in part (a).
Since the tangent line to the curve
Substitute
Isolate y,
Thus, the equation of the tangent line is
(c)
To sketch: The graph of the tangent line and the curve. Check zoom in the graph toward the point (1, 0) until the curve and the tangent line is indistinguishable.
(c)
Explanation of Solution
The equation of the tangent line
The equation of the given curve is
Use the online graphing calculator to draw the graph of the functions as shown below in Figure 1.
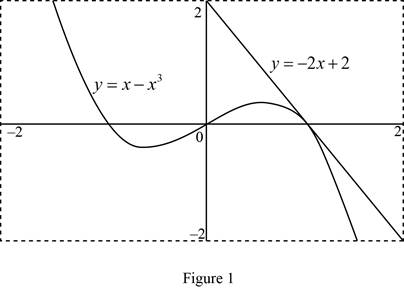
Graph:
Use the online graphing calculator to zoom toward the point (1, 0) as shown below in Figure 2.
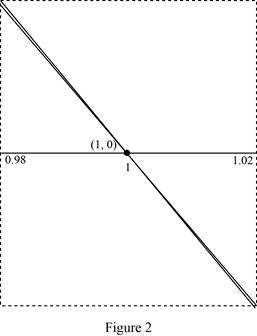
From Figure 2, it is observed that when zoom in the graph toward the point (1, 0), the graph of the tangent line and the curve looks likes almost identical.
Hence, it is verified that the graph of the tangent line and the curve zooming toward the point (1, 0) until the tangent line are indistinguishable.
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





