Chapter 2, Problem 8P

(a)

To determine

To Sketch: A continuous function with domain [0,1] and range is also lies in [0,1]. It has fixed point.

Answer to Problem 8P

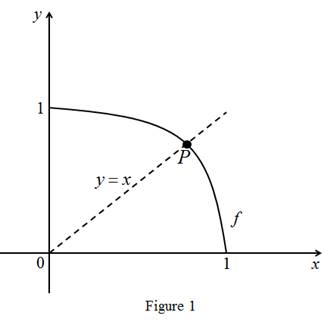
Explanation of Solution

The graph of the curve is $y=x$ at the fixed point p. The function f is continuous at p.

The function f continuous with domain [0,1] and range is also lies in [0,1].

(b)

To determine

To Draw: A continuous function with domain [0,1] and range is also lies in [0,1]. It does not have fixed point.

Explanation of Solution

There is no possible to draw the graph of the continuous function with domain [0,1] and range is also lies in [0,1]. It does not have fixed point.

Because, the “obstacle” is the line $y=x$. Any intersection of the graph of the line $y=x$ continuous at the fixed point p. If the graph doesn’t cross the line somewhere in $\left(0,1\right)$, then it must either start at $\left(0,0\right)$ or finish at $\left(1,1\right)$.

(c)

To determine

To prove: Any continuous function with domain [0,1] and range in [0,1] must have a fixed point.

Explanation of Solution

Result used: The intermediate value theorem,

If $f\left(x\right)$ is a continuous function on $\left[a,b\right]$, then for every w between $f\left(a\right)$ and $f\left(b\right)$, there exist a value c in between a and b such that $f\left(c\right)=w$.

Proof:

Consider the function $F\left(x\right)=f\left(x\right)-x$ Any continuous function with domain [0,1] and range in [0,1].

Now need prove f has a fixed point that means if $f\left(0\right)=0$ then f has a fixed point.

Assume that $f\left(0\right)\ne 0$ and in the same way assume that $f\left(1\right)\ne 1$, then

$\begin{array}{l}F\left(0\right)=f\left(0\right)-0\\ F\left(0\right)=f\left(0\right)>0\end{array}$

and $F\left(1\right)=f\left(1\right)-1<0$.

By the intermediate value theorem, there exist some number c in the interval $\left(0,1\right)$  such that $F\left(c\right)=f\left(c\right)-c$.

So $f\left(c\right)=c$.

Therefore f has a fixed point c.

Hence proved.