
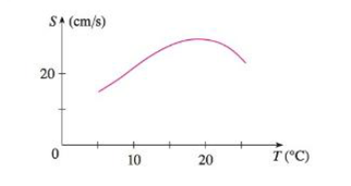
The graph shows the influence of the temperature T on the maximum sustainable swimming speed S of Coho salmon.
(a) What is the meaning of the derivative S'(T)? What are its units?
(b) Estimate the values of S'(15) and S'(25) and interpret them.
(a)
The derivative
Explanation of Solution
Given:
The influence of the temperature T on the maximum sustainable swimming speed S of coho salmon.
Calculation:
The maximum sustainable swimming speed S is depends on the influence of the temperature T.
The maximum sustainable swimming speed
Note that, the derivative
The derivative
The instantaneous rate of change is equal to
Here
Thus, the units are centimeter per second per centigrade.
Therefore, the unit are
(b)
To estimate: The value of
Explanation of Solution
Estimate the value of
Form given Figure, it is observed that the tangent line at 15 is passing through the point
The slope of the tangent line to the curve at 15 as follows,
Thus, the slope of the tangent line to the curve at 15 is,
Note that, the slope of the tangent line to the curve at 15 is same
Therefore,
Estimate the value of
Form given Figure, it is observed that the tangent line at 25 is passing through the point
The slope of the tangent line to the curve at 25 as follows,
Thus, the slope of the tangent line to the curve at 25 is,
Note that, the slope of the tangent line to the curve at 25 is same as
Therefore,
The derivative
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Calculus Early Transcendentals, Binder Ready Version
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
Calculus: Early Transcendentals (3rd Edition)
Finite Mathematics and Calculus with Applications (10th Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





