
Concept explainers
Area of a Kite A kite frame is to be made from six pieces of wood. The four pieces that form its border have been cut to the lengths indicated in the figure. Let x be as shown in the figure
- (a) Show that the area of the kite is given by the function
- (b) How long should each of the two crosspieces be to maximize the area of the kite?
(a)
To show: The area function of the kite is
Explanation of Solution
The kite contains four triangles with finite lengths is shown below,
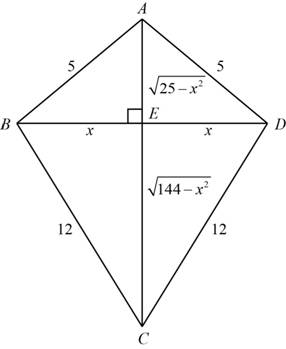
Figure (1)
In
Use the Pythagoras theorem to find the length AE,
In
Use the Pythagoras theorem to find the length CE,
The formula to calculate the area of triangle is,
The formula to calculate area of kite,
Thus, the area function of the kite is
(b)
To find: The length of the cross pieces of the kite to maximize the area of the kite.
Answer to Problem 32P
The length of the two cross pieces are
Explanation of Solution
Given:
The given kite frame to be made from six pieces of wood is shown below,

Figure (1)
From the part (a), the area function is
To find the lengths of the cross pieces of the kite which maximize the area of the kite, it needs to draw the graph of the function
The function contains the variable x is length of the horizontal cross piece.
The local maximum value of the function is the maximum finite value where the value of the function at the any number is greater than to the original function.
The condition for local minimum is,
The graph of the function is shown below.
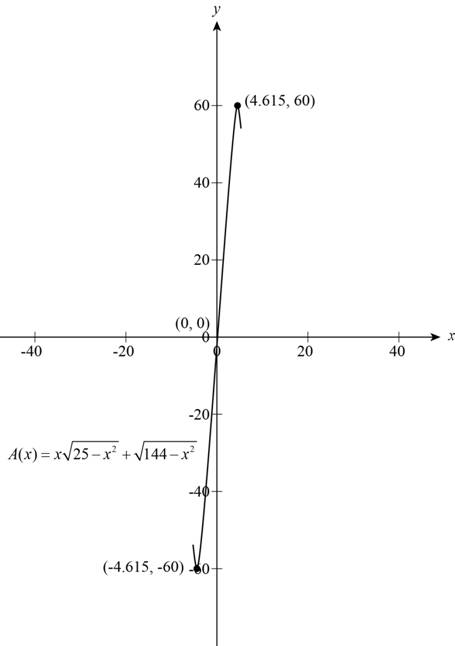
Figure (2)
From the graph of the function shown as Figure (2) the greatest peak of the graph at the point
Then, the maximum area of the kite is
The length of the side BD in the figure (1) is,
Substitute 4.979 for x in the value of
The length of the side AC in the figure (1) is
Now, substitute 4.979 for x in the length of the side AC.
So, the original value of x is
Thus, the value of one cross piece is
Chapter 2 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





