
Concept explainers
(a)
To express: The monthly cost in terms of the distance driven d assuming the function follows a linear function.
(a)
Answer to Problem 18E
The equation of the monthly cost in terms of the distance driven d is
Explanation of Solution
Let d represents the number of miles driven in a month and C represents the monthly cost in dollars.
Recall the general equation of the linear function
Since the cost function follows a linear function, the equation of the cost C in terms of the number of miles driven d is in the form of
According to the given data, there are two points such as (480, 380) and (800, 460).
Obtain the slope m by using the two point formula as follows.
Thus, the slope is
Use the slope
Thus, the required equation is
(b)
To predict: The monthly cost of driving 1500 miles.
(b)
Answer to Problem 18E
The monthly cost of driving 1500 miles is $635.
Explanation of Solution
From part (a), the equation of the monthly cost in terms of the distance driven d is
Substitute
Thus, the cost of driving 500 miles is $635.
(c)
To sketch: The graph of the cost as a function of distance driven and interpret the slope.
(c)
Explanation of Solution
Let x-axis represents the number of miles driven and y-axis represents the monthly cost in dollars.
From part (a), the equation of the monthly cost as a function of distance driven is
Obtain the values of C for several values of d as tabulated in Table 1 and draw the graph as shown below in Figure 1.
| d | C |
| 0 | 260 |
| 500 | 385 |
| 1000 | 510 |
Table 1
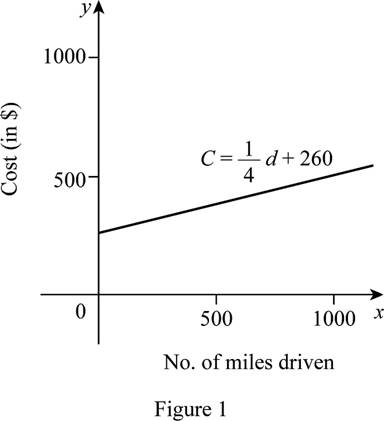
From Figure 1, it is observed that the graph is a straight line as the function is linear.
Also, notice that the cost increases as the number of miles increases. That is, if the distance driven increases by 320, then the cost increases by $80 ($0.25 per mile.)
Thus, the slope is,
(d)
To explain: The meaning of C-intercept.
(d)
Answer to Problem 18E
The C-intercept of the cost function is 260 and it represents the fixed manufacturing cost per day.
Explanation of Solution
From part (a), the equation of the monthly cost as a function of the distance driven is
Since it follows a linear function, the constant term c is considered as the y-intercept.
Thus, the y-intercept is 260.
The C-intercept represents the fixed monthly cost as it is the constant term.
(e)
To explain: Why a linear function is suitable for this model.
(e)
Explanation of Solution
Since the monthly cost is fixed and the cost increases as the distance driven increases, the function follows the linear function.
Thus, the linear function is suitable for this situation.
Chapter 1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





