
Concept explainers
(a)
To find: The amount remaining isotope of sodium after 60 hours.
(a)
Answer to Problem 32E
The amount remaining isotope of sodium after 60 hours is 0.125g.
Explanation of Solution
Given:
The half-life of sodium is 15 hours.
The mass of sample sodium = 2g.
Calculation:
Let
That is
After 15 hours the amount of sodium is
Substitute 2g for
After 30 hours the amount of sodium
Substitute 1g for
After 45 hours the amount of sodium is
Substitute 0.5g for
After 60 hours the amount of sodium is
Substitute 0.25g for
Therefore, the amount sodium after 60 hours is 0.125g.
(b)
To find: The amount of sodium after t hours.
(b)
Answer to Problem 32E
After t hours amount of sodium is
Explanation of Solution
Calculation:
Consider half –life sodium amount in 15 hours =
Where
After
Therefore after t hours amount of sodium as follows,
Substitute
Therefore, after t hours amount of sodium is
(c)
To estimate: The remaining amount of sodium after 4 days.
(c)
Answer to Problem 32E
After 4days the amount of sodium is
Explanation of Solution
Given:
Consider after 15 hours the amount of sodium = 1g.
Calculation:
After 15 hours the amount of sodium is
By using part (b) solution
Obtain the amount after 4 days that means 96 hours.
Substitute 96 for t in
Therefore, after 4 days the amount of sodium is
(d)
To estimate: The amount of bismuth reduced to 0.01g.
(d)
Answer to Problem 32E
The amount of sodium amount reduced to 0.01g for 38.2215 days.
Explanation of Solution
Given:
The reduced amount of sodium = 0.01g.
Graph:
Let x axis for hours and y axis for sodium (g).
Use the online graphing calculator and draw the graphs for sodium level and hours as shown below Figure 1.
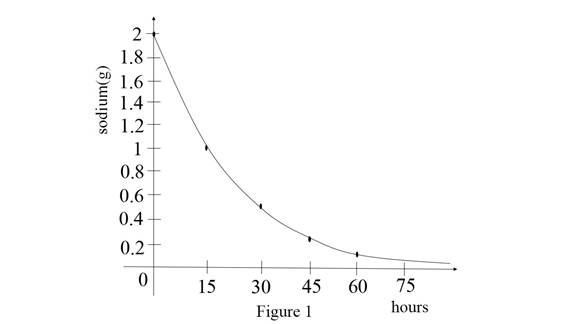
Observe the graph an initial stage sodium amount is 2g.
Then after 15 hours the mass is reducing to 1g.
After 30 hours the mass is reducing to 0.5g.
After 45 hours mass is reducing to 0.25g.
After 60 hours mass is reducing to 0.125g.
Therefore, the mass of sodium is reducing when the hours are increasing.
Calculation:
From the graph, the general form of sodium after t hours
Substitute 0.01 for
Take naturel logarithm on both sides,
Simplify further,
Therefore, the amount of sodium reduced to 0.01g for 114.6645 hours.
Chapter 1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





