
Concept explainers
(a)
To express: The distance in terms of the time elapsed.
(a)
Answer to Problem 14E
The distance d in terms of time elapsed is,
Explanation of Solution
Let d be the distance traveled in miles and the t be the time elapsed in hours.
When t = 0, the distance is 0 which can be expressed as (0, 0).
Since he passes the Ann Arbor at 50 minutes, t = 50 minutes or
The distance traveled is 40 miles. That is, at
Use the obtained two points and find the slope m as follows.
Thus, the slope
Use the slope
Thus, the required function is
(b)
To sketch: The graph of the distance equation obtained in part (a).
(b)
Explanation of Solution
Let x-axis be represented the time in hours and the y-axis be represented the distance in miles.
Given that the distance function of elapsed time is
Obtain the value of d for various values of t and draw the graph of d as shown below in Figure 1.
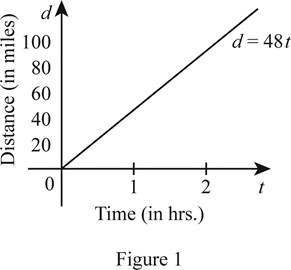
From Figure 1, it is observed that function is a linear function.
(c)
To find: The slope of the graph drawn in part (b); explain the meaning of slope.
(c)
Answer to Problem 14E
The slope is 48, which represents the rate of change of the distance in miles.
Explanation of Solution
The equation
Thus, the slope of the Figure 1 shown in part (b) is 48. It represents that the rate of change of the distance in miles.
Moreover, it is observed that there is a decrease in the distance when time increases and hence it is in direct variation. The distance covered in an hour is 48 miles.
Chapter 1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





