
(a)
To write: An equation of the exponential function with base
(a)
Answer to Problem 5E
The equation that defines the exponential function is
Explanation of Solution
An exponential function is a function of the form
The equation of the exponential function with base
Notice that this function is not defined when
Therefore, the equation of the exponential function with base
(b)
The domain of the exponential function obtained in part (a).
(b)
Answer to Problem 5E
The domain of the exponential function
Explanation of Solution
The domain of a function is defined as the set of all possible values of the independent variable of the function for which the function is defined.
Consider the exponential function
Since the function
Therefore, the domain of the exponential function
(c)
The range of the function
(c)
Answer to Problem 5E
The range of the function
Explanation of Solution
The range of a function is defined as the set of all possible values of the dependent variable of the function.
Consider the exponential function
Since
So the range of the function is the set of all positive real values.
Therefore, the range of the function
(d)
(i)
To sketch: The graph of the exponential function if
(d)
(i)
Explanation of Solution
The graph of the exponential function
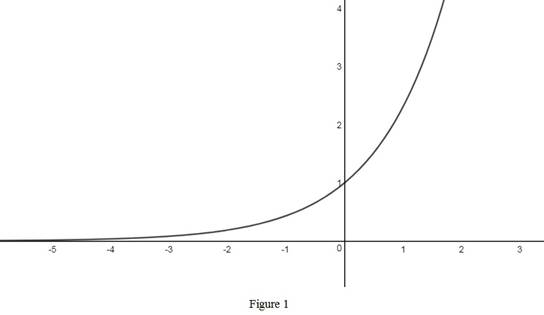
From Figure 1, it is observed that the graph is monotonically increasing.
(ii)
To sketch: The graph of the exponential function if
(ii)
Explanation of Solution
The graph of the exponential function

From Figure 2, it is observed that the graph is parallel to x-axis as the function is a constant.
(iii)
To sketch: The graph of the exponential function if
(iii)
Explanation of Solution
The graph of the exponential function
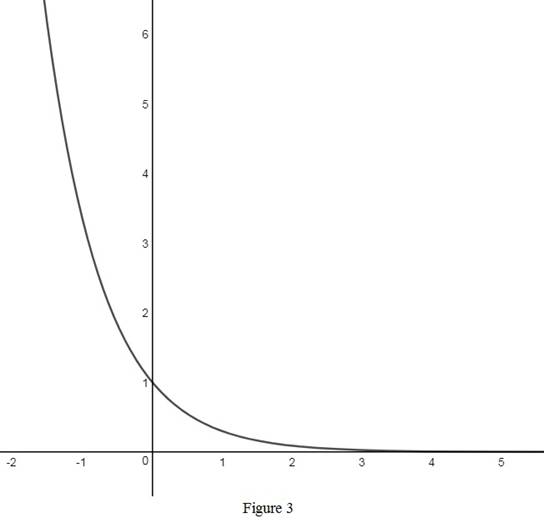
From Figure 3, it is observed that the graph is monotonically decreasing.
Chapter 1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





