
Concept explainers
(a)
To sketch: The points P and Q in the coordinate plane.
(a)
Explanation of Solution
The given points is
In point
The coordinate plane of two given points is shown below,
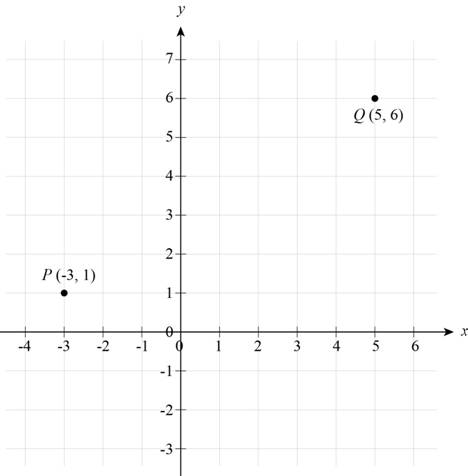
Figure (1)
Figure (1) shows the points
(b)
To find: The distance between
(b)
Answer to Problem 17T
The distance between P and Q is
Explanation of Solution
Given:
The points is
Calculation:
The distance formula of two points
Where,
Substitute 5 for
Thus, the distance between P and Q is
(c)
To find: The midpoint of line segment PQ.
(c)
Answer to Problem 17T
The midpoint of segment PQ is
Explanation of Solution
Given:
The points is
Calculation:
The formula of line segment from
Substitute 5 for
Thus, the midpoint of segment PQ is
(d)
To find: The slope of line passes through two pints P and Q.
(d)
Answer to Problem 17T
The slope of line PQ is
Explanation of Solution
Given:
The points is
Calculation:
The formula of slope of line passes through two points is,
In above formula m is slope of line and
Substitute 6 for
Thus, the slope of line PQ is
(e)
To find: The perpendicular bisector of line PQ.
(e)
Answer to Problem 17T
The equation of perpendicular bisector is
Explanation of Solution
Given:
The points is
Calculation:
The slope of line passes through points
The lines are perpendicular if,
Where,
Substitute
The slope
The formula of
Substitute
Thus, the equation of perpendicular bisector is
(f)
To find: The equation of circle with diameter PQ.
(f)
Answer to Problem 17T
The equation of circle is
Explanation of Solution
Given:
The points is
Calculation:
The equation of circle with center
The distance between points
The radius of circle is half of diameter that is,
The line segment PQ is a diameter of circle and the midpoint of line segment PQ is center of circle that is
Substitute 1 for h,
Thus, the equation of circle is
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





