
To calculate: The solution of the given inequality and express the solution using interval notation. Also graph the solution set on the real number line.
Answer to Problem 92RE
In order to solve an inequality, the following things can be done.
• Add the same number to each side of the inequality.
• Subtract the same number from each side.
• Multiply or divide each side by the same number and if multiplied or divided each side by a negative number, then the inequality symbol must be reversed.
The inequality can be solved as follows:
The solution using interval notation is
The shaded region shows solution of the given inequality on the graph below .
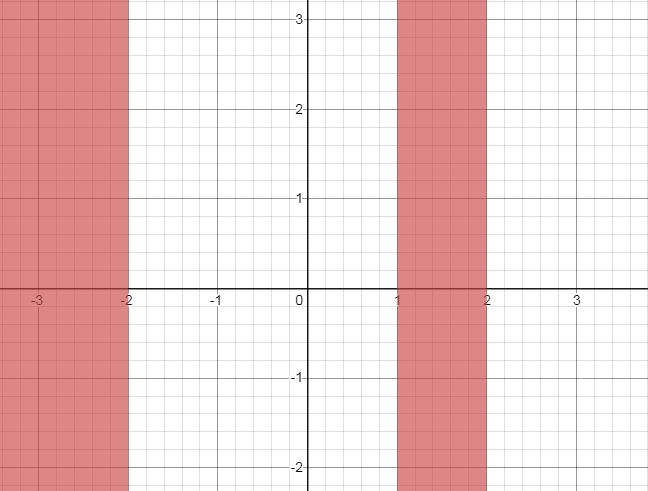
Explanation of Solution
Given information:
The given inequality is
Formula used:
In order to solve an inequality, the following things can be done.
• Add the same quantity to each side of the inequality.
• Subtract the same quantity from each side.
• Multiply or divide each side by the same positive quantity and If multiplied or divided each side by a negative quantity, then the inequality symbol must be reversed.
In case of non linear inequality,the function may be factorised and solved further long division method etc.
Calculation:
In order to solve an inequality, the following things can be done.
• Add the same quantity to each side of the inequality.
• Subtract the same quantity from each side.
• Multiply or divide each side by the same positive quantity and If multiplied or divided each side by a negative quantity, then the inequality symbol must be reversed.
The inequality can be solved as follows:
The solution using interval notation is
The shaded region shows the given inequality on the graph below:
Calculation:
In order to solve an inequality, the following things can be done.
• Add the same quantity to each side of the inequality.
• Subtract the same quantity from each side.
• Multiply or divide each side by the same positive quantity and If multiplied or divided each side by a negative quantity, then the inequality symbol must be reversed.
The inequality can be solved as follows:
The solution using interval notation is
The shaded region shows the given inequality on the graph below:
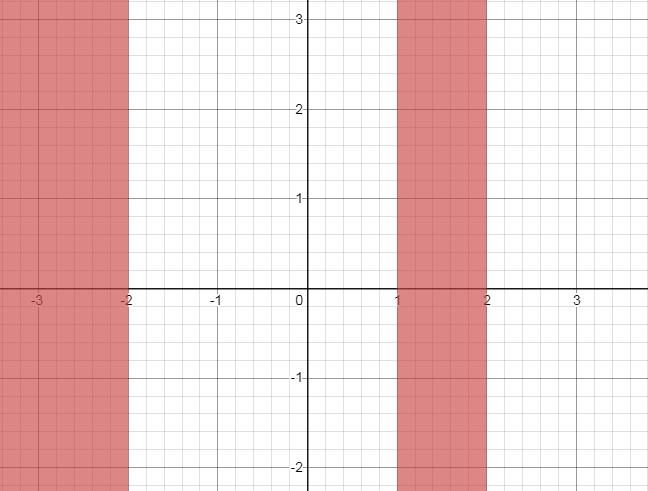 ..
..
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





