
To calculate: The new coordinates of the point
Answer to Problem 117E
The new coordinates of the point
Explanation of Solution
Given information:
In the coordinate plane y -axis acts a mirror and reflect each point to the right of it into a point left of it.
Calculation:
Consider the point
From the above translation it clear that x- coordinate of each point becomes negative and y -coordinate remains the same.
So, the point
Thus, the new coordinates of the point
To calculate: The new coordinates of the point
Answer to Problem 117E
The new coordinates of the point
Explanation of Solution
Given information:
In the coordinate plane y -axis acts a mirror and reflect each point to the right of it into a point left of it.
Calculation:
Consider the point
From the above translation it clear that x- coordinate of each point becomes negative and y -coordinate remains the same.
So, the point
Thus, the new coordinates of the point
To calculate: The old coordinates of the point
Answer to Problem 117E
The old coordinates of the point
Explanation of Solution
Given information:
In the coordinate plane y -axis acts a mirror and reflect each point to the right of it into a point left of it.
Calculation:
Consider the point
From the above translation it clear that x- coordinate of each point becomes negative and y -coordinate remains the same.
So, the point
Thus, the old coordinates of the point
To calculate: The new coordinates of the points
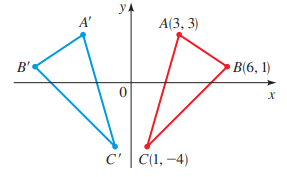
Answer to Problem 117E
The new coordinates of the points
Explanation of Solution
Given information:
In the coordinate plane y -axis acts a mirror and reflect each point to the right of it into a point left of it.
Calculation:
Consider the triangle
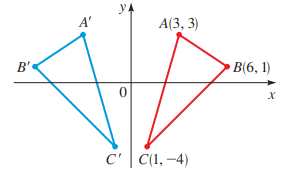
It is provided that in the coordinate plane y -axis acts a mirror and reflect each point to the right of it into a point left of it.
From the above translation it clear that x- coordinate of each point becomes negative and y -coordinate remains the same.
So, the point
So, the point
So, the point
Thus, the new coordinates of the points
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





