
Concept explainers
a.
Find a linear equation that relates
a.
Answer to Problem 75E
Explanation of Solution
Calculation:
The cost of driving
The cost of driving
The cost and distance are considered coordinates. The slope of the line is
So, the line joining the points is
Where
Hence, the linear equation that relates
b.
Use part
b.
Answer to Problem 75E
Explanation of Solution
Calculation:
When
Hence, the cost of driving
c.
Draw the graph of the linear equation. What does the slope of the line represent?
c.
Answer to Problem 75E
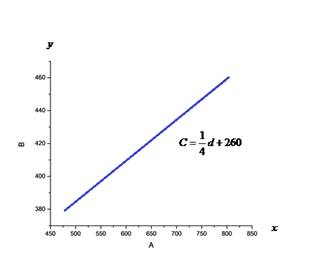
The slope represents cost per mile.
Explanation of Solution
Calculation:
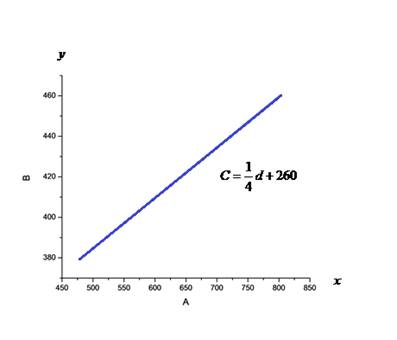
Note that the cost is represented on
Hence, the slope represents cost per mile.
d.
What does
d.
Answer to Problem 75E
The
Explanation of Solution
Calculation:
When
which represents the monthly rental spent toward the car.
Hence, the
e.
Why is a linear relationship a suitable model for this situation?
e.
Answer to Problem 75E
A linear fuction gives a suitable model because we would expect the cost of driving to be more or less proportional to the number of miles driven.
Explanation of Solution
Calculation:
A linear fuction gives a suitable model because we would expect the cost of driving to be more or less proportional to the number of miles driven.
Hence, a linear relationship is a suitable model for this situation.
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





