
To solve: the nonlinear inequality. Express the solution using interval notation and graph the solution set.
Answer to Problem 60E
Explanation of Solution
Given:
The given inequality is
Concept used:
Guidelines for solving nonlinear inequality:
- Move all terms to one side.
- Factor the non-zero side of the inequality.
- Find the value for which each factor is zero. The number will divide the real lines into interval. List the interval determined by these numbers
- Make a table or diagram by using test values of the signs of each factor on each interval. In the last row of the table determining the sign of the product of these factors.
- Determine the solution of the inequality from the last row of the sign table.
Calculation:
The given inequality can be expressed as
Firstto find the zeros of the expression in the numerator and demniminator, then
From the two zeros above, it extracts the following intervals:
Now, make a table by using test values of the signs of each factor on each interval.
| + | + | ||
| + | |||
| quotient | + | + |
As it is seen that quotient is less thanin the interval
Hence,the solution set is
The graph of the non-linear inequality
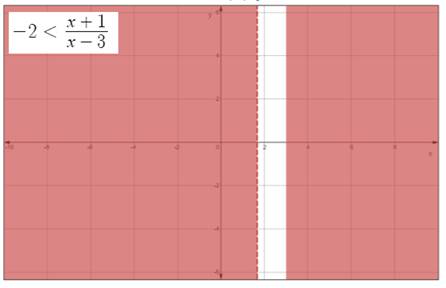
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





